|
DOI: 10.25136/2409-8736.2017.2.23067
Дата направления статьи в редакцию:
19-05-2017
Дата публикации:
28-06-2017
Аннотация:
Предметом данного исследования является процесс обучения студентов-математиков базовой дисциплине «Численные методы». В статье приведены основные подходы к обучению численным методам. В качестве гипотезы выдвинуто предположение, что от уровня развития вычислительного мышления зависит мотивация к обучению дисциплине, необходимое время для изучения и понимания материала курса. Авторами уточнено понятие «вычислительного мышления», как когнитивного мыслительного процесса, определены способности, которые необходимо развивать для формирования вычислительного мышления студентов, предложены методы и средства, которые необходимо использовать при организации процесса обучения. В качестве основных методов организации учебной деятельности авторами рассматриваются метод системной динамики и динамической визуализации. В качестве основных средств предлагаются ментальные карты и анимация, которые с позиций информационного подхода являются наиболее эффективным средством визуализации информации. Основным выводом проведенного исследования является тот факт, что предложенные методы и средства существенно влияют на развитие выделенных компонент вычислительного мышления студентов, а, следовательно, и на успешность обучения курсу «Численные методы». Это подтвердил педагогический эксперимент, проведенный в Сибирском федеральном университете.
Ключевые слова:
вычислительное мышление, численные методы, методы обучения, средства обучения, динамическая визуализация, метод системной динамики, ментальные карты, алгоритмическое мышление, абстракция, электронный курс
УДК: 37.03
Abstract: The subject of the research is to study the process of teaching the basic discipline “Numerical Methods” to the students of mathematics. The paper provides the main approaches to teaching of numerical methods. The hypothesis is made that motivation to learning the discipline, necessary time for examination and understanding of material of the course depends on the level of development of numerical cognition. The authors clarify the notion of "numerical cognition" as a cognitive process, determine the abilities needed to develop the numerical cognition of students, as well as propose tools for organizing the learning process. Methods of system dynamics and dynamic visualization are used for organizing the educational activity. As the key means, the authors also review the mental maps and animation, which from the perspective of information approach represent most efficient tool for visualization of information. The main conclusion of the conducted research lies in the fact that the suggested methods and means significantly affect the development of identified components of numerical cognition of students, and therefore, the successful studying of the course “Numerical Methods”. This has been confirmed by the pedagogical experiment carried out in the Siberian Federal University.
Keywords: numerical cognition , numerical methods, learning methods, teaching means, dynamic visualization, methods of system dynamics, mental maps, algorithmic thinking, abstraction, e-course
Введение
Одним из базовых курсов при подготовке специалистов по направлению 02.03.01 «Математика и компьютерные науки» является дисциплина «Численные методы», обеспечивающая связь теоретической математики и программирования.
Отбору и формированию содержания курса «Численные методы» для студентов вузов посвящены труды многих российских ученых. В первую очередь это: Самарский А.А., Марчук Г.И., Тихонов А.Н., Бахвалов Н.С., Калиткин Н.Н., Годунов С.К., Воеводин В.В., Гельфанд И.М., Дородницын А.А., Березин И.С., Белоцерковский О.М., Жидков Н.П., Яненко Н.Н., Фадеев Д.К., Фадеева В.Н. и др. Учебники этих авторов многократно переиздаются и являются фундаментальной основой при разработке учебных программ по дисциплине «Численные методы». Однако в них не затрагиваются вопросы практической реализации численных методов с использованием современных компьютерных технологий.
С появлением компьютеров главной особенностью обучения численным методам стало использование специализированных математических пакетов и систем программирования для решения прикладных задач. Современные численные методы в совокупности с возможностью их автоматизации при использовании персональных компьютеров превратились в рабочий инструмент для решения задач научного, технического, экономического и др. характера. В печати стали появляться издания с примерами конкретных алгоритмов и текстов программ с краткими предварительными сведениями по теории используемых методов, ориентированные на среду разработки. Эти издания чаще всего проигрывают в математическом обосновании идей и применимости численных методов, но помогают студентам при разработке собственных программ на одном из языков программирования. Учебники такого плана в большинстве своем являются переводными, но есть среди них и русские авторы: Мудров А.Е, Турчак Л.И., Плотников П.В., Зализняк В.Е. и др.
Основной задачей при обучении курсу «Численные методы» в современных условиях является задача обучить студентов не столько основным численным методам решения классических задач математики и математической физики, сколько сформировать у них навыки и умения построения и реализации алгоритма решения профильных задач с помощью компьютерных технологий. Это возможно лишь при достаточно высоком уровне развития вычислительного мышления обучаемых.
В диссертационных исследованиях Беленковой И.В., Беликова В.В., Кузнецовой И.А., Пальчиковой H.H., Рябухиной Е.А., Рябых A.B., Степановой Т.А., Сушенцова А.А., Федченко Г.М. и др. предложены различные методики обучения студентов численным методам. Однако в упомянутых работах не рассматривается взаимосвязь уровня знаний по численным методам и уровнем развития вычислительного мышления обучаемых. Тем не менее, именно от уровня развития вычислительного мышления зависит и мотивация к обучению численным методам, и необходимое время для изучения и понимания материала курса и другие психологические и личностные факторы студента. В этой связи представляет интерес поиск новых подходов и дидактических приемов организации и проведения учебного процесса по курсу «Численные методы», нацеленных на развитие вычислительного мышления студентов-математиков.
Вычислительное мышление
Анализ подходов к понятию «вычислительное мышление» [2] и основ информационного подхода к обучению [3] позволил определить вычислительное мышление, как когнитивный мыслительный процесс решения задач, который включает в себя:
- формулировку проблемы таким образом, чтобы ее решение основывалось на использовании компьютера (К);
- логическую организацию и анализ данных (Д);
- представление данных с помощью абстракций (АБ);
- автоматизацию данных на основе алгоритмического мышления (АЛ);
- обобщение, выявление и использование шаблонов (ОБ).
Таким образом, для развития вычислительного мышления требуется формировать у студентов следующие способности:
- Способность к логической организации и анализу данных. Использование вычислительных технологий для сбора, создания и анализа данных. Умение управлять, делать выводы из полученных данных, визуализировать данные.
- Способность мыслить абстрактно. Умение мыслить на разных уровнях абстракции и легко переходить с одного на другой при разработке программы. Определение общих характеристик во множестве объектов и игнорирование несущественных различий между ними. Выражение этих характеристик в виде математического понятия либо описания объекта при программировании. Умение для описания конкретного решения выбрать соответствующий уровень абстракции языка. Создание единого набора инструкций для манипулирования объектами разных типов, в котором различия в способах воздействия на разные объекты определяются нижними уровнями абстракции.
- Способность мыслить алгоритмически. Умениеоблечь абстрактную идею в последовательность шагов, необходимых для её практической реализации.
- Способность к компьютерной реализации решения проблемы. Реализация алгоритмов численных методов на языке высокого уровня или с использованием математических пакетов.
- Способность обобщать и выявлять шаблоны при решении задач. То есть умение переходить на более высокую ступень абстракции путем выявления общих признаков предметов рассматриваемой области, в общем случае переходя в процессе обобщения по цепочке: единичное понятие – обобщенное понятие – суждение – закон – теория.
Возникает вопрос, какие методы (процессы) и средства (инструменты) необходимо использовать для организации обучения численным методам, нацеленного на развитие вычислительного мышления?
Методы и средства организации учебной деятельности
Традиционные методы организации учебной деятельности, определяющие «знаниевый» подход, направлены на формирование теоретического мышления. Они определяют последовательность изложения материала от «простого» к «сложному», на основе чего осуществляются все основные операции мышления, такие как индукция, дедукция, анализ, синтез, обобщение. Однако, этих методов недостаточно для развития вычислительного мышления.
Поэтому кроме традиционных в качестве основных методов организации учебной деятельности по дисциплине «Численные методы» нами использованы метод системной динамики и динамической визуализации. Кроме традиционных средств обучения (учебные пособия, программное обеспечение для разработки численных методов, электронные тренажеры) в исследовании выделены ментальные карты и электронный курс по дисциплине «Численные методы». На рисунке 1 представлена схема применения предложенных методов и средств при обучении численным методам. Основным отличием этих методов и средств является их нацеленность на формирование и развитие вычислительного мышления.
|
методы
|
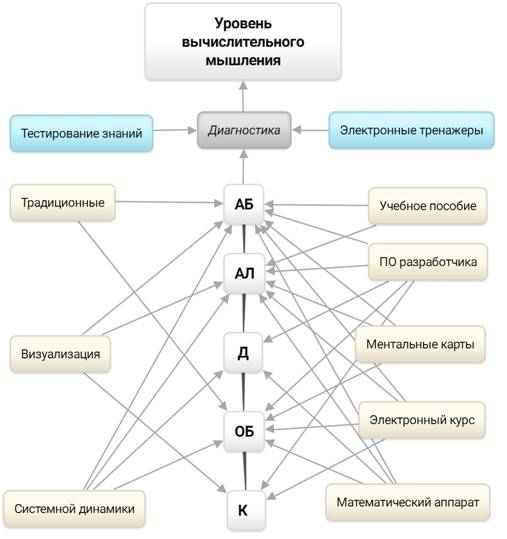
|
средства
|
Рис. 1 – Методы и средства обучения численным методам
Системная динамика – это метод построения и изучения поведения сложных систем с течением времени в зависимости от структуры этой системы и взаимодействия ее элементов. Ряд исследователей [4] отмечают, что это способствует развитию чувственной памяти, интуитивному стилю мышления и формированию ментальных схем, отражающих алгоритмические действия.
Технология визуализации – процесс представления данных в виде изображений, обеспечивающий максимальное удобство для понимания и придания зримой формы любому мыслительному объекту, субъекту, процессу и т.д. С точки зрения Вербицкого А.А. [1] метод визуализации «способствует формированию профессионального мышления за счет систематизации, концентрации и выделения наиболее значимых, существенных элементов содержания обучения».
Ментальные карты и анимация с позиций информационного подхода являются наиболее эффективным средством визуализации информации. Они позволяют сформировать образы абстрактных математических понятий, повысить степень запоминания схем вычислений на интуитивном уровне, представить целостную картину применения численных методов в профессиональной деятельности.
Обучение студентов-математиков численным методам осуществляется с использованием электронного курса, реализованного на открытой платформе Moodle. Для теоретической подготовки студентов используется элемент курса «Лекция», центральным элементом которого являются ментальные карты (рис. 2), которые позволяют преподавателю в визуальной форме структурировать информацию, наглядно в сжатом виде изложить суть и содержание лекции, определить основные понятия, сформулировать постановку задачи и методы ее решения, установить связь с раннее изученными методами.
Рис. 2 – Пример фрагмента ментальной карты при изучении численных методов
Для понимания работы численных методов на языке JavaScript реализованы элементы динамической визуализации, позволяющие продемонстрировать работу численных методов. Использование ментальных карт и динамической визуализации повышает качество понимания студентами абстрактных понятий, развивает их абстрактное мышление и понимание алгоритмов численных методов.
Практическая подготовка студентов по дисциплине «Численные методы» направлена на разработку алгоритмов численных методов с использованием языков программирования или математических пакетов по желанию студента. Умение строить тестовые задачи, анализировать их устойчивость, сходимость, оценивать полученные результаты работы программы существенно сокращает сроки выполнения лабораторных работ. При реализации численного метода студент рассматривает задачу с точки зрения трех уровней абстракции: постановка математической задачи, численный метод решения и программная реализация. Написание программы в виде отдельных логических модулей позволяет студенту сводить решение к более простым для выполнения задачам или к ранее решенным, обобщать методы для решения широкого класса задач с учетом возможности расширяемости.
Выводы
Проведенный в Сибирском федеральном университете педагогический эксперимент показал, что предложенные методы и средства, существенно влияют на развитие выделенных элементов вычислительного мышления студентов, а, следовательно, и на успешность обучения курсу «Численные методы»
Библиография
1. Вербицкий А.А. Активное обучение в высшей школе: контекстный подход. – М.: «Высшая школа», 1991. – 207 с.
2. Клунникова, М.М. О подходах к определению понятия «вычислительное мышление». / М.М. Клунникова, Т.П. Пушкарева // Инновации в образовательном пространстве: опыт, проблемы, перспективы: сб. науч. ст., 2016. – С. 35-39.
3. Пак Н.И. О концепции информационного подхода в обучении / Н.И. Пак // Вестник Красноярского государственного педагогического университета им. В.П. Астафьева. 2011. № 1. – С. 91-97.
4. Пак Н.И. Развитие интуиции и параллельного мышления методом системной динамики / Н.И. Пак // Вестник Красноярского государственного педагогического университета им. В.П. Астафьева. 2012. № 2 (20). – С. 117-123.
References
1. Verbitskii A.A. Aktivnoe obuchenie v vysshei shkole: kontekstnyi podkhod. – M.: «Vysshaya shkola», 1991. – 207 s.
2. Klunnikova, M.M. O podkhodakh k opredeleniyu ponyatiya «vychislitel'noe myshlenie». / M.M. Klunnikova, T.P. Pushkareva // Innovatsii v obrazovatel'nom prostranstve: opyt, problemy, perspektivy: sb. nauch. st., 2016. – S. 35-39.
3. Pak N.I. O kontseptsii informatsionnogo podkhoda v obuchenii / N.I. Pak // Vestnik Krasnoyarskogo gosudarstvennogo pedagogicheskogo universiteta im. V.P. Astaf'eva. 2011. № 1. – S. 91-97.
4. Pak N.I. Razvitie intuitsii i parallel'nogo myshleniya metodom sistemnoi dinamiki / N.I. Pak // Vestnik Krasnoyarskogo gosudarstvennogo pedagogicheskogo universiteta im. V.P. Astaf'eva. 2012. № 2 (20). – S. 117-123.
|
 Перевести страницу на:
Перевести страницу на:










 Перевести страницу на:
Перевести страницу на:










 Статья опубликована с лицензией Creative Commons Attribution-NonCommercial 4.0 International License (CC BY-NC 4.0) – Лицензия «С указанием авторства – Некоммерческая».
Статья опубликована с лицензией Creative Commons Attribution-NonCommercial 4.0 International License (CC BY-NC 4.0) – Лицензия «С указанием авторства – Некоммерческая».
