Инструментальное средство автоматизированного рефакторинга UML-диаграмм классов по заданным критериям качества

Концепция MDA ^[1], предложенная Object Management Group (OMG), предполагает разработку сложной программной системы на высоком уровне абстрагирования – PIM (Platform Independent Model), а затем автоматической генерации одной или нескольких PSM (Platform Specific Model).

Таким образом, группой OMG была предложена исследовательская программа, связанная с вопросами создания, трансформации, анализа, хранения и передачи моделей программных систем. Основными стандартами, предложенными в рамках MDA, являются MOF ^[2], UML^[3], XMI ^[4] и др.

MOF спецификация, разработана для описания метамоделей языков MDA. В основе MOF лежит подмножество языка UML 2.

XMI специально разработан для обмена моделями между инструментальными средствами.

Как указывается в документе, XMI предоставляет:

• представление объектов в терминах XML элементов и атрибутов;
• стандартные механизмы связи объектов в одном файле или между несколькими файлами;
• валидацию XMI документов с использованием XML схем;
• идентификацию объектов посредством обращения к ним через ID или UUID.

Синтаксис XMI-документа описан в спецификации при помощи EBNF.

UML – унифицированный графический язык моделирования, позволяющий описывать программные системы, бизнес процессы и т.д. UML можно использовать как для спецификации моделей для последующей разработки системы, так и для реконструкции моделей уже существующих систем.

Для моделирования системы при помощи UML используются следующие диаграммы:

• диаграммадеятельности (Activity Diagram);
• диаграмма классов (Class Diagram);
• диаграмма коммуникации (Communication Diagram);
• диаграмма компонентов (Component Diagram);
• диаграмма составной структуры (Composite Structure Diagram);
• диаграмма развёртывания (Deployment Diagram);
• диаграмма общего взаимодействия (Interaction Overview Diagram);
• диаграмма объектов (Object Diagram);
• диаграмма пакетов (Package Diagram);
• диаграмма профилей (Profile Diagram);
• диаграммасостояний (State Machine Diagram);
• диаграмма прецедентов (Use Case Diagram).

Одними из основных диаграмм при проектировании являются UML-диаграммы классов, описывающие систему как набор классов, интерфейсов и отношений между ними.

К актуальным вопросам предложенной OMG исследовательской программы относится задача автоматизированного рефакторинга UML-диаграмм классов. Решить данную задачу необходимо для создания инструментальных средств анализа и трансформации UML-диаграмм классов.

На сегодняшний день существует два основных подхода к рефакторингу UML-модели программного обеспечения.

Первый связан с поисковой программной инженерией ^[5] (SBSE), интерес к которой все возрастает в последнее время. В SBSE задачи программной инженерии формулируются как задачи оптимизации, которые затем решаются поисковыми алгоритмами (ГА, симуляция отжига, алгоритмы роевого интеллекта и т.д.) SBSE используется для решения задачи рефакторинга UML-диаграмм классов в работах ^[6-11].

К инструментам, разрабатываемым в рамках данного подхода, можно отнести Dearthóir ^[12], Darwin ^[8], CODe-Imp ^[13], Bunch tool ^[14] и др.

Недостатком подхода является произвольное, зачастую лишенное смысла применение трансформаций к элементам диаграммы классов. Кроме того, авторы используют в том числе и паттерны, применение которых на этапе проектирования вызывает сомнения (например, применение паттерна Адаптер).

Второй возможный подход связан с разработкой фреймфорков автоматизированного рефакторинга, в которых ведущая роль отдается проектировщику системы. В то время как фреймворк применяет трансформации, используя определенные правила трансформации во взаимодействии с проектировщиком.

Цель данной работы — предложить абстрактную структуру данных UMLMap, удобную для анализа и трансформации UML-диаграмм классов; алгоритмы анализа UML-диаграмм классов, необходимые для решения задачи автоматизированного рефакторинга UML-диаграмм классов; а также представить инструментальное средство автоматизированного рефакторинга UML-диаграмм классов UML Refactoring Tool ^[15].

Пусть `d` ­— это UML -диаграмма классов `d={C,I,R}` , где `C` — множество классов `C={x_(0),...c_(k)}` , `I` — множество интерфейсов `I={i_(0),...i_(1)}` , `R` — множество отношений `R={r_(0),...r_(g)}.`

Пусть `c_(i)` ­— это класс `c_(i)={A_(i),M_(i),F_(i)}` , где `A_(i)` — множество атрибутов `A_(i)={a_(0)^(i),a_(1)^(i),...,a_(n)^(i)},` `M_(i)` — множество методов `M_(i)={m_(0)^(i),m_(1)^(i),...,m_(m)^(i)}` , `F_(i)` — множество свойств `F_(i)={st_(i), v_(i),abs_(i),...}, st_(i) in{0,1}` — признак статичности, `v_(i)` — параметр видимости `v_(i) in {public,private,protected}` , `abs_(i)` — признак абстрактности `abs_(i) in {0,1}.`

Пусть `i_(i)` ­— интерфейс, описывающий множество методов `M_(i)={m_(0)^(i),m_(1)^(i),...m_(m)^(i)}.`

Определение 1

Трансформацией UML-диаграммы классов назовём функцию отображения следующего вида:

`t(d,E): d-> d'`

где `E` – множество элементов диаграммы` e_(i) in d, e_(i) in {C,R,I}.`

Определение 2

Трансформация UML-диаграммы классов `t(d,E): d -> d'` является семантически эквивалентной, если :

`S(d)` ~ `S(d')` ,

где ­`S(d)` — значение структурной семантики диаграммы `d` , которое может быть описано следующим образом:

`S_(i)={{c_(1)^(i)={...},c_(2)^(i)={...},...,c_(k)^(i)={...}}, {i_(2)^(i)={...},...i_(l)^(i)={...}},{r_(1)^(i),r_(2)^(i),...,r_(m)^(i)}},`

где `c_(1),...,c_(k) in d_(i)` — классы диаграммы `d_(i)` ;`i_(1),...,i_(l)` — интерфейсы диаграммы `d_(i)` ; `r_(1),...,r_(m) in d_(i)` — отношения диаграммы `d_(i)`.

Тогда задача автоматического рефакторинга может быть сформулирована следующим образом:

Пусть дана UML-диаграмма классов `d` , множество семантически эквивалентных трансформаций `T `и целевая функция `f(d).`

Требуется найти такое множество пар `{t,E}` , что:

`d'=t(d,E), ` ∆`f(d) < 0.`

Для того, чтобы обеспечить удобство и эффективность трансформации и анализа UML-диаграмм классов была предложена абстрактная структура данных UMLMap (см. рис. 1), хранящая хеш-таблицы классов, отношений и интерфейсов диаграммы.

К примеру, сложность поиска класса с xmi:id = “X” в XMIдокументе оценивается как `O(n)` , в то время, как в хеш-таблице, хранящей пары {ключ, значение}, сложность поиска оценивается как `O(1).`

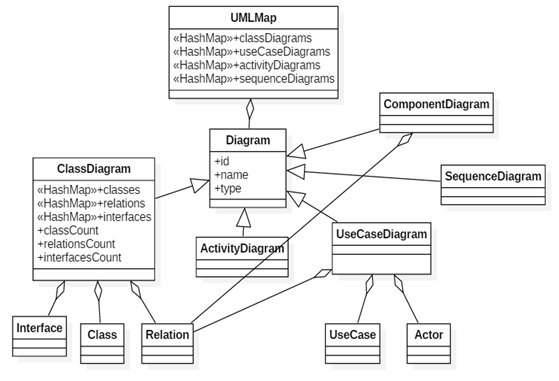
Рис. 1. Сокращённая диаграмма классов для абстрактной структуры данных UMLMap

Для возможности импортирования и экспортирования XMI документов был разработан специальный транслятор.

На основе предложенной структуры данных удобно осуществлять анализ диаграмм классов, их трансформацию, а также расчёт метрик.

Трансформация «Стратегия» означает инкапсуляцию нескольких алгоритмов для обеспечения их взаимозаменяемости (см. рис. 2 и рис. 3).

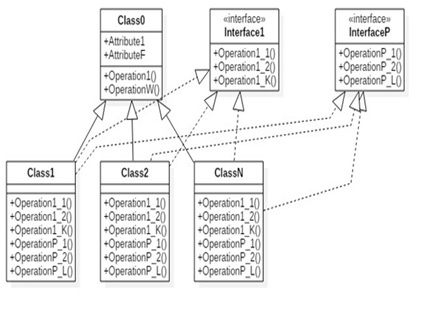
Рис. 2. Предпосылки к применению трансформации «Стратегия»

Алгоритм поиска множеств элементов диаграммы `E` , к которым может быть применена трансформация «Стратегия», описывается следующим образом:

1. Для каждого класса диаграммы найти те, у которых есть потомки, и добавить их в хеш-таблицу <Class, List<Class>> `l_(1)={c_(i),{c_(i1),c_(i2),...},...}.`

2. Для каждого класса из `l_(1)` проверить, реализуют ли его потомки какие-либо интерфейсы. Если да — добавить их в хеш-таблицу <Class,List<Class>> `l_(2)={c_(i),{i_(i1),i_(i2),...},...}.`

3. Для каждого класса из `l_(2)` рассчитать ∆`f(d)` . Если ∆`f(d)<0` — добавить в список `l_(3) ` = {parent_id, {child_classes_ids}, {interfaces_ids}}.

4. Вернуть `l_(3)` .

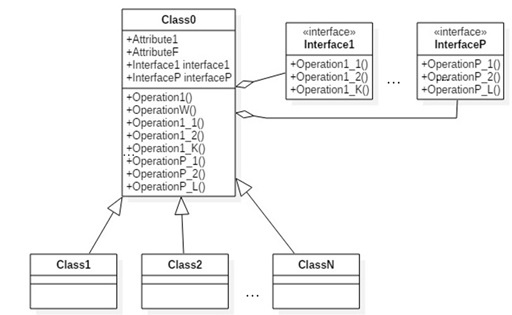
Рис. 3. Результат применения трансформации «Стратегия»

Для абстрактной структуры данных UML Map алгоритм может быть описан следующим образом:

График, отображающий зависимость времени работы алгоритма от размера UML-диаграммы классов показан на рис. 4. Время было рассчитано как среднее арифметическое времени, измеренного на 100 запусках алгоритма для UML-диаграмм классов размером 10, 20, 40, 100, 150, 200, 250, 300 классов. Из графика следует, что сложность алгоритма по времени выполнения оценивается `O(n).`

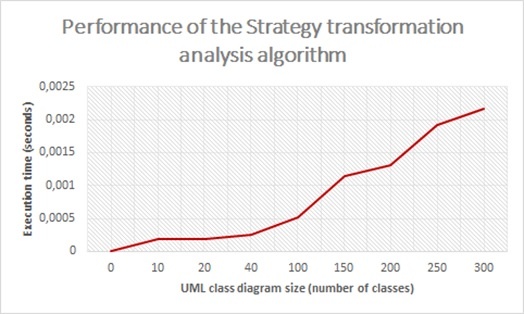
Рис. 4. Зависимость времени работы алгоритма анализа для трансформации «Стратегия» от размера UML-диаграммы классов

Трансформация «Введение интерфейса» предполагает создание промежуточного слоя между классами, которые реализуют множество методов `M` и классами, которые вызывают данные методы посредством отношений типа dependency `r_(i)` .

Алгоритм поиска множеств элементов диаграммы `E` , к которым может быть применена трансформация «Введение интерфейса», может быть описан следующим образом:

1. Найти все классы `c_(i) in d` ,которые не реализуют ни одного интерфейса, и добавить их к списку `l_(1)`.

2. Среди классов из списка `l_(1)` найти те `c_(i)` , которые участвуют в отношениях dependency вида: `c_(j) -> c_(i)` и добавить их в список `l(2)` .

3. Для каждого класса `c_(i)` вычислить ∆`f(d)` .

4. Вернуть все `c_(i)` , для которых ∆`f(d)<0` .

Для абстрактной структуры данных UML Map алгоритм может быть описан следующим образом:

График, отображающий зависимость времени работы алгоритма от размера UML-диаграммы классов показан на рис. 5. Время было рассчитано как среднее арифметическое времени, измеренного на 100 запусках алгоритма для UML-диаграмм классов размером 10, 20, 40, 100, 150, 200, 250, 300 классов. Из графика следует, что сложность алгоритма по времени выполнения оценивается `O(n).`

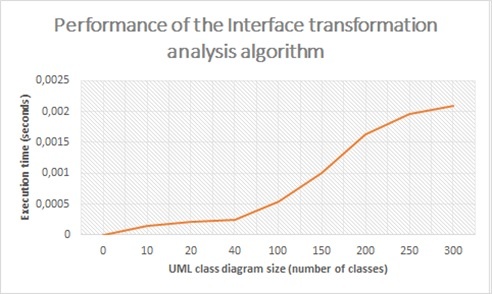
Рис. 5. Зависимость времени работы алгоритма анализа для трансформации «Введение интерфейса» от размера UML-диаграммы классов

В качестве примера целевой функции рефакторинга UML-диаграмм классов рассмотрим метрику структурной сложности UML-диаграмм классов `K(d)`:

`K(d)=k_(1)*|C|+k_(2)*|I|+k_(3)*|R|+k_(4)*sum_(i=0)^n|A_(i)|+k_(5)*sum_(i=0)^n|M_(i)|+k_(6)*sum_(j=0)^m|M_(j)'|,`

где `K(d)` — структурная сложность диаграммы `d;` `|C|` — число классов `c_(i)in d;` `|I|` — число интерфейсов `i_(i) in d` ; `|R|` — число отношений `r_(i) in d`; `A_(i)` — множество атрибутов `a_(j) in c_(i), c_(i) in d`; `M_(i)` — множество методов классов (за исключением методов, которые принадлежат интерфейсам, имплементируемым классами) `m_(i) in c_(i), c_(i) in d`; `M_(j)'` — множество методов интерфейсов `m_(j) in i_(i), i_(i) in d` ; `k_(1), k_(2), k_(3), k_(4), k_(5), k_(6)` — веса для каждой группы элементов диаграммы.

Для решения задачи автоматизированного рефакторинга UML-диаграмм классов было разработано инструментальное средство UML Refactoring.

Основные функциональные элементы представлены на рис. 6.

Пользователю предоставляется работать с файлами диаграмм: импортировать и экспортировать из формата XMI, сохранять преобразованные диаграммы и открывать их во внутреннем формате umlr.

После открытия файла диаграмма классов представляется в оперативной памяти в форме АСД UMLMap, основанной на хеш-таблицах. Затем OOMCalculator производит расчет объектно-ориентированных метрик и выводит результат на экране. Analyzer производит поиск трансформаций, снижающих значение целевой функции. Выбранная пользователем трансформация применяется к диаграмме классом Transformer. После чего заново производится расчет метрик и поиск трансформаций.

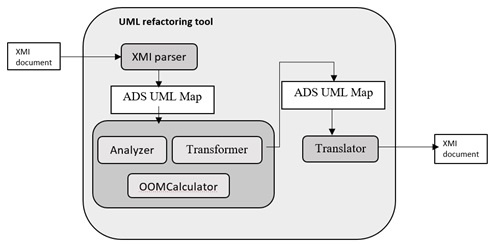
Рис. 6. Функциональные элементы программы UMLRefactoring

Пусть дана UMLдиаграмма (см. рис. 7).

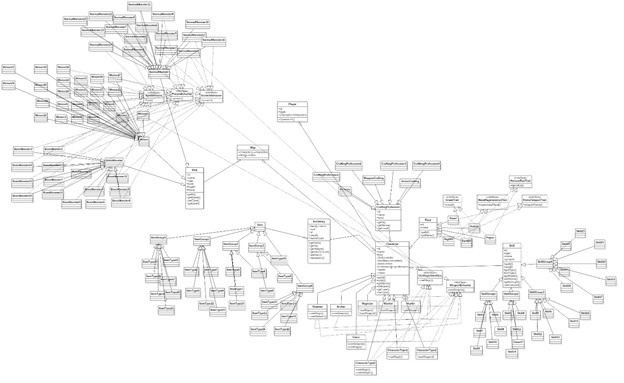
Рис. 7. UML-диаграмма классов `d_(1)`

Результат анализа диаграммы `d_(1)` показан на рис. 8. В диаграмме 150 классов, 9 интерфейсов, 197 отношений. Значение метрики Diagram Structural Complexity (DSC) = 198.86.

После применения к диаграмме `d_(1)` одной из предложенных трансформация значение метрики DSC становится равно 187.9.

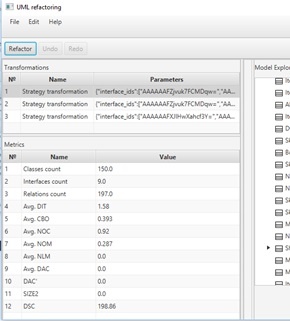
Рис. 8. Результат анализа диаграммы `d_(1)` при помощи инструментального средства UML Refactoring Tool

Результат применения трансформации «Стратегия» показан на рис. 9.

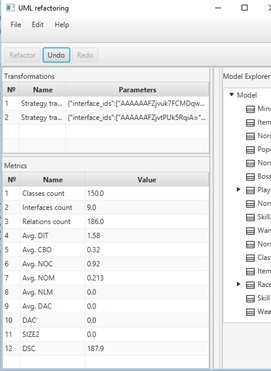
Рис. 9. Результат применения трансформации «Стратегия» к диаграмме классов `d_(1)`

Для удобства трансформации и анализа UML-диаграмм классов в работе предложена абстрактная структура данных UMLMap, хранящая основные элементы UML-диаграмм классов в хеш-таблицах.

Кроме того, сформулированы алгоритмы анализа UML-диаграммы классов для применения трансформаций «Стратегия» и «Введение интерфейса», определяющие те элементы диаграммы, применение трансформаций к которым снижает значение целевой функции `f(d)` .

В ходе вычислительного эксперимента установлено, что вычислительная сложность предложенных алгоритмов оценивается

Кроме того, в работе представлено инструментальное средство автоматизированного рефакторинга UML-диаграмм классов UML Refactoring Tool, позволяющее экспортировать диаграммы классов в программу из XMI-документов, производить расчет основных объектно-ориентированных метрик. Кроме того, пользователю формируется таблица трансформаций, применение которых снижает значение целевой функции. При выборе одной из трансформаций, она автоматически применяется к диаграмме. Существует возможность сохранения диаграмм во внутреннем формате инструментального средства или экспорта их в формат XMI.