|
DOI: 10.7256/2306-4188.2014.4.13274
Дата направления статьи в редакцию:
24-10-2014
Дата публикации:
07-11-2014
Аннотация:
Различные элементы учебного материала имеют неодинаковую важность для понимания последующих вопросов изучаемого курса и выполнения заданий итогового контроля. Используя метод экспертных оценок, в принципе можно определить важность того или иного вопроса. Предметом исследования является процесс изучения учеником последовательности вопросов неодинаковой важности. На изучение важных вопросов должно быть отведено больше времени, а некоторые вопросы, значение которых мало, вообще не следует рассматривать. Статья посвящена проблеме оптимизации времени изучения отдельных элементов учебного материала различной важности, при которой результат обучения достигает максимума. Для решения сформулированной выше оптимизационной задачи использовались методы системного анализа, математического и компьютерного моделирования, алгоритмизации и программирования. Научная новизна работы заключается в следующем: 1) впервые сформулирована проблема оптимизации времени изучения элементов учебного материала различной важности; 2) проведена серия вычислительных экспериментов, в ходе которых получено несколько оптимальных распределений времени изучения вопросов различной важности при тех или иных параметрах модели; 3) на основе анализа полученных результатов установлены закономерности оптимального распределения времени и уровня усвоения учащимися вопросов, имеющих различную важность.
Ключевые слова:
дидактика, теория обучения, компьютерное моделирование, оптимизация, дидактическая система, учебный материал, время изучения, кибернетика, эффективность обучения, математические методы
УДК: 37.02
Abstract: Different elements of the educational material have different importance for learning the following topics and passing the final tests. By using the method of expert evaluation, it is possible to define how important this or that element is. The subject of the present research is the process of learning a sequence of topics of different importance. Some important topics require more time to be learnt while other topic that are not important should be even ignored. The present article is devoted to the problem of optimization of time required to learn particular elements of educational material of different importance in order to achieve the best learning efficiency. To achieve the aforesaid objectives, the author has used the methods of systems analysis, mathematical and computer simulation, algorithmization adn programming. The scientific novelty of the research is caused by the following: 1) for the first time in the academic literature the author raises the problem of optimization of time required to learn educational material of different importance; 2) the author has carried out a number of simulation experiments to define the best time distribution in the process of learning topics of difference importance; 3) based on the results, the author describes the rules for the best time distribution and efficient learning of topics of different importance.
Keywords: didactic method, learning theory, computer simulation, optimization, didactic system, educational material, time required to learn the material, cybernetics, learning efficiency, mathematical methods
1. Введение Дальнейшее развитие математической теории обучения требует комплексного подхода к изучению системы “учитель–ученик” [4]. Среди современных методов исследования педагогических систем особое положение занимают методы математического и имитационного (или компьютерного) моделирования. Их сущность состоит в том, что реальная педагогическая система заменяется абстрактной моделью, –– некоторым идеализированным объектом, который повторяет наиболее существенные свойства изучаемой системы. При этом исследуется поведение модели с помощью математических методов [1–2, 5, 8] и компьютерной имитации [3, 5–7]. Последнее означает создание компьютерной программы, которая ведет себя подобно исследуемой системе, и проведение серии вычислительных экспериментов при различных параметрах, начальных условиях и внешних воздействиях. Применяются многокомпонентные модели обучения [6, 7], автоматный подход [1, 5, 8], мультиагентное моделирование [3], при котором каждый учащийся заменяется программным агентом, функционирующим независимо от других агентов. Основная задача имитационного моделирования процесса обучения состоит в том, чтобы, зная параметры учащихся, характеристики используемых методов и распределение учебной информации (программу обучения), определить уровень знаний или сформированности навыка у учащихся в последующие моменты времени.
Важным направлением дидактики является оптимизация процесса обучения, нахождение таких форм и методов организации учебного процесса, при которых функционирование системы образования было бы наиболее эффективным, то есть при наименьших затратах приносило бы максимальную пользу. Оптимизационная задача [5, с. 86–90] в общем случае заключается в нахождении параметров учебного процесса (распределения учебного материала, длительности и количества занятий, зависимости уровня требований учителя от времени и т.д.), при которых уровень знаний учащихся в конце обучения достигнет заданного значения, а сам процесс обучения будет удовлетворять наложенным ограничениям на затраты времени и усилий.
Частным случаем этой общей оптимизационной задачи является проблема нахождения оптимального распределения времени изучения элементов учебного материала различной важности. Будем считать, что коэффициент важности ЭУМ тем выше, чем больше необходимость данного ЭУМ для понимания последующих вопросов этой и других дисциплин. Можно предположить, что в конце курса проводится тестирование, в ходе которого в первую очередь проверяется знание наиболее важных вопросов. Коэффициент важности для каждого ЭУМ может быть определен, например, методом экспертных оценок.
2. Поиск оптимального времени изучения ЭУМ различной важности Дидактическая система “учитель–ученик” относится к самонастраиваемым системам управления. Учитель выбирает такие методы обучения, при которых ученик достигает требуемых результатов и выполняет учебную программу. При этом он стремится минимизировать суммарные усилия и затраты времени на обучение, максимизируя целевую функцию –– уровень знаний ученика Z. Ученик в свою очередь так организует свою деятельность, чтобы минимизировать разность между уровнем требований учителя U и уровнем приобретенных знаний Z (или степенью выполнения учебного задания). Установив оптимальные условия обучения, получаем траекторию, по которой должна в идеале развиваться система “учитель–ученик”.
Допустим, учебный курс включает в себя N=100 элементов учебного материала (ЭУМ) e1, e2, …, eN, и заканчивается тестированием. ЭУМ имеют одинаковую сложность, но различную важность Vi, которая зависит от степени использования данного ЭУМ при решении задач, усвоении последующих вопросов, выполнении заданий теста. Если Vi = 0, то важность i–ого ЭУМ минимальна, то есть его изучать в рамках данного курса не нужно. При Vi = 1 важность i–ого ЭУМ максимальна; его изучение необходимо для понимания последующих вопросов и выполнения заданий итогового контроля. Пусть курс содержит N ЭУМ различной важности; будем считать, что она связана с номером ЭУМ i соотношением: Vi =i/N. Время изучения i–ого ЭУМ обозначим через ti. Общее время изучения T, равное сумме всех ti (i =1, 2, …, N) остается постоянным, коэффициент усвоения A учащегося задан. Общий результат обучения (и тестирования) R равен взвешенной сумме произведений уровня усвоения Zi каждого ЭУМ на их важность Vi.
Необходимо: 1) определить оптимальные значения ti длительностей изучения каждого ЭУМ, при которых результат тестирования R будет максимальным; 2) получить соответствующую зависимость уровня знаний Zi ученика от важности Vi рассмотренных вопросов; 3) изучить зависимость распределения времени ti изучения ЭУМ от их важности Vi при различных коэффициентах усвоения A и продолжительностях обучения T.
Будем исходить из того, что знания ученика Zi увеличиваются со скоростью, пропорциональной разности (U-Zi), а забывания не происходит. Получаем дифференциальное уравнение [5–7]: dZi /dt = A(U–Zi). Уровень требований учителя U для каждого ЭУМ равен 1. При этом знания Zi i–ого ЭУМ в результате обучения увеличиваются от 0 (ЭУМ совсем не изучен) до некоторого значения, не превышающего 1. Максимально возможное значение Zi равно 1, что соответствует полному изучению i–ого ЭУМ. Приращение знаний за время dt равно A(U–Zi)dt. Рассматриваемое дифференциальное уравнение можно записать в конечных разностях и составить алгоритм для его численного решения.
Программа должна моделировать изучение первого ЭУМ в течение времени t1, затем изучение второго ЭУМ в течение времени t2 и т.д., изучение N–ого ЭУМ в течение времени tN. При этом общее время прохождения курса T остается постоянным. Будем считать, что результаты R тестирования пропорциональны взвешенной сумме знаний ученика всех N ЭУМ с учетом их важности: R=V1*Z1+…+Vi*Zi +…ZN*VN, где Zi –– знания учеником i–ого ЭУМ из интервала 0-1. Определив уровень усвоения каждого ЭУМ, можно рассчитать R в конце обучения. Чтобы решить рассматриваемую оптимизационную задачу, необходимо многократно случайным образом варьировать время ti изучения i–ого ЭУМ и принимать такие значения ti, при которых результат тестирования R в конце обучения становится выше.
В рассматриваемой математической модели используются формулы:
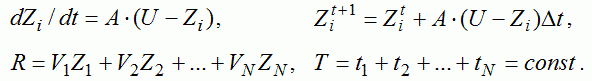
3. Компьютерная программа Задача состоит в определении таких значений ti (i = 1, 2, …, N), при которых R достигает максимума. Компьютерная программа ПР–1, написанная на языке Pascal, решает данную оптимизационную задачу. Она содержит:
1. Блок задания параметров модели, в котором задаются: 1) коэффициент усвоения A ученика; 2) количество N изучаемых ЭУМ; 3) общее время обучения T; 4) важность каждого ЭУМ Vi, которая равномерно растет от 0 до 1 с шагом 1/N по закону Vi = i / N; 5) начальные значения оптимизируемых переменных ti (время изучения i–ого вопроса). В программе ПР–1 N=50, T=50 УЕВ (усл. ед. времени), ti = T / N = 1 УЕВ (усл. ед. времени).
2. Процедуру Obuchen, в которой осуществляется моделирование обучения. Она, исходя из известных ti, определяет уровень знаний ученика Zi по каждому i–ому вопросу, а также результат тестирования R.
3. Процедуру Grafik, которая очищает экран и строит графики: 1) зависимости ti(Vi) времени изучения различных ЭУМ от их важности; 2) зависимости Zi(Vi) уровня знаний среднестатистическим учеником различных ЭУМ от их важности Vi после прохождения обучения.

4. Цикл Repeat … until, в котором собственно и осуществляется поиск оптимального распределения времени изучения ЭУМ различной важности. В нем: 1) случайным образом выбираются 5 ЭУМ, изменяются их время изучения ti на небольшие случайные величины; 2) пересчитываются все остальные ti так, чтобы их сумма оставалась равной T; для этого в цикле вычисляются новые значения t’i =ti*T / T’, где T’ – сумма всех ti после их изменений; 3) снова моделируется изучение N вопросов (процедура Obuchen;) и определяется его результат R’; 4) полученное значение R’ сравнивается с предыдущим; если оно увеличилось, то изменения принимаются, а иначе –– отвергаются. Эта последовательность действий многократно повторяется до тех пор, пока результат тестирования R не достигнет максимума.
Общее время изучения T = t1+t2+…+tN всего курса и коэффициент усвоения учащегося A заданы. Необходимо: 1) определить оптимальные значения длительностей изучения каждого вопроса, при которых результаты тестирования R ученика в конце обучения будет максимальными; 2) изучить зависимость ti(Vi) распределения времени изучения ЭУМ от их важности при различных коэффициентах усвоения A; 3) получить соответствующую зависимость Zi(Vi) уровня усвоения учеником изучаемых вопросов от их важности.
4. Результаты оптимизации времени изучения Так как забывания не происходит, сложность всех ЭУМ одинакова и не зависит ранее изученных вопросов, то и результат моделирования не будет зависеть от того, в каком порядке изучаются рассматриваемые N элементов учебного материала.
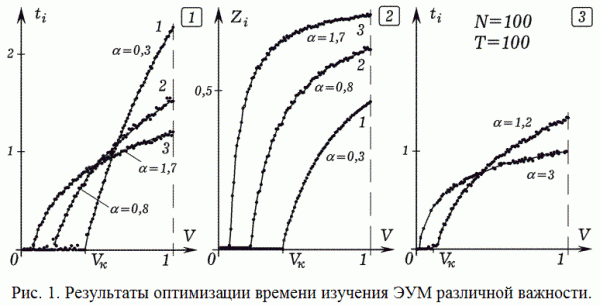
В результате работы программы ПР–1 строятся графики ti(Vi) и Zi(Vi) в случае, когда результат тестирования R конце обучения максимален. При N=100, T=100 УЕВ, получаются кривые, изображенные на рис. 1. Для каждого A существует критический уровень важности Vk; те вопросы, у которых V<Vk, изучать не следует (ti=0). При низком коэффициенте усвоения A=0,3 нужно изучать лишь те вопросы, важность которых велика, затрачивая на них больше времени (рис. 1.1, кривая 1). Вопросы, имеющие важность Vi < 0,55, изучать не следует. При увеличении A ученик быстрее усваивает информацию, поэтому критический уровень важности Vk снижается (кривые 2 и 3, соответствующие A=0,8 и 1,7). При оптимальном обучении для любых A уровень усвоения ЭУМ по мере увеличения их важности растет (рис. 1.2). Так как вопросы, важность которых ниже Vk, не изучались, то соответствующий уровень их усвоения Zi равен 0.
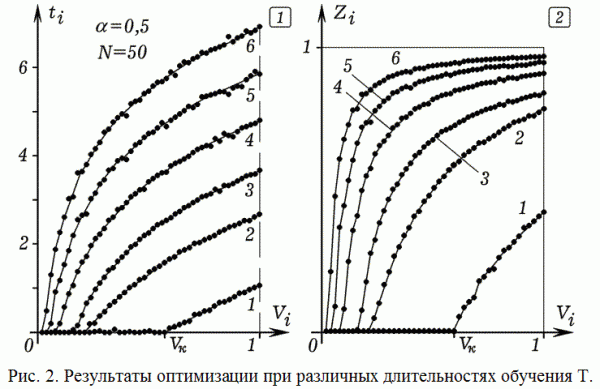
На рис. 2 представлены кривые ti(Vi) и Zi(Vi), получающиеся в результате решения рассматриваемой оптимизационной задачи при N=50 и различных длительностях обучения T. Графики 1, 2, …, 6 соответствуют T=10, 50, 100, 150, 200, 250. Из них видно, что при увеличении T критическое значение Vk смещается влево, число не изучаемых вопросов с низкой важностью V<Vk уменьшается. Время изучения ti каждого ЭУМ с V>Vk растет, уровень его усвоения учащимся Zi также увеличивается, стремясь к 1.
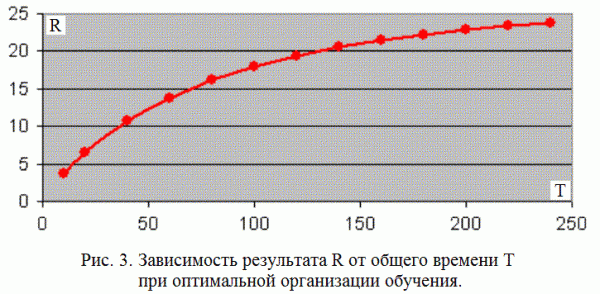
Если провести серию вычислительных экспериментов при различных значениях T, то можно получить график зависимости оптимального результата тестирования R от общего времени T изучения курса (рис. 3). Получается возрастающая кривая, которая при увеличении T стремится к некоторому пределу. Аналогичный результат имеет место при фиксированных N, T и изменяющемся коэффициенте усвоения A.
Выводы Обсуждаемая модель процесса обучения позволила исследовать зависимость оптимального распределения времени изучения отдельных вопросов (ЭУМ) от параметров A, N, T. Было установлено следующее: 1) характер распределения ti(Vi) сильно зависит от соотношения коэффициента усвоения ученика A, количества изучаемых вопросов N и длительности обучения T; 2) для конкретного набора A, N, T существует критическое значение важности Vk; вопросы с V<Vk изучать не следует; 2) при уменьшении A, T и увеличении N критическое значение Vk растет, поэтому следует изучать только ЭУМ, имеющие высокую важность; 3) при больших A, T и небольших N следует изучать как важные, так и не очень важные ЭУМ; при этом на более важные вопросы необходимо затрачивать больше времени, чем на менее важные; 4) оптимальное распределение уровня усвоения учеником различных ЭУМ в зависимости от их важности характеризуется возрастающей функцией Zi(Vi); 5) при увеличении коэффициента усвоения A и времени изучения курса T уровень усвоения учащимся изучаемых вопросов увеличивается, общий результат обучения (и тестирования) R возрастает, стремясь к некоторому предельному значению. Полученные решения рассматриваемой оптимизационной задачи соответствуют основным положениям теории обучения.
Библиография
1. Кудрявцев В.Б., Вашик К., Строгалов А.С., Алисейчик П.А., Перетрухин В.В. Об автоматном моделировании процесса обучения. – Дискретная математика. – 1996. – Т. 8., вып. 4. – C. 3 – 10.
2. Леонтьев Л.П., Гохман О.Г. Проблемы управления учебным процессом: Математические модели. – Рига, 1984. – 239 с.
3. Ивашкин Ю.А., Назойкин Е.А. Мультиагентное имитационное моделирование процесса накопления знаний // Программные продукты и системы. – 2011. – N 1. – С. 47 – 52.
4. Комарцова Л.Г., Лавренков Ю.Н., Антипова О.В.. Комплексный подход к исследованию сложных систем // Программные системы и вычислительные методы. – 2013. – № 4. – С. 330-334. DOI: 10.7256/2305-6061.2013.4.10551.
5. Майер Р.В. Кибернетическая педагогика: Имитационное моделирование процесса обучения. – Глазов: ГГПИ, 2013. – 138 с. (http://maier-rv.glazov.net)
6. Майер Р.В. Многокомпонентная модель обучения и ее использование для исследования дидактических систем // Фундаментальные исследования: Педагогические науки. – 2013. – N 10. – С. 2524 – 2528.
7. Майер Р.В. Основная задача математической теории обучения и ее решение методом имитационного моделирования // Международный журнал прикладных и фундаментальных исследований. – 2014. – № 2 – С. 36 – 39. URL://www.rae.ru/upfs/?section=content&op=show_article&articleid=5002
8. Соловов А.В., Меньшиков А.А. Дискретные математические модели в исследования процессов автоматизированного обучения // Educational Technology & Society. – 2001. – N 4. – С. 205 – 210.
References
1. Kudryavtsev V.B., Vashik K., Strogalov A.S., Aliseichik P.A., Peretrukhin V.V. Ob avtomatnom modelirovanii protsessa obucheniya. – Diskretnaya matematika. – 1996. – T. 8., vyp. 4. – C. 3 – 10.
2. Leont'ev L.P., Gokhman O.G. Problemy upravleniya uchebnym protsessom: Matematicheskie modeli. – Riga, 1984. – 239 s.
3. Ivashkin Yu.A., Nazoikin E.A. Mul'tiagentnoe imitatsionnoe modelirovanie protsessa nakopleniya znanii // Programmnye produkty i sistemy. – 2011. – N 1. – S. 47 – 52.
4. Komartsova L.G., Lavrenkov Yu.N., Antipova O.V.. Kompleksnyi podkhod k issledovaniyu slozhnykh sistem // Programmnye sistemy i vychislitel'nye metody. – 2013. – № 4. – S. 330-334. DOI: 10.7256/2305-6061.2013.4.10551.
5. Maier R.V. Kiberneticheskaya pedagogika: Imitatsionnoe modelirovanie protsessa obucheniya. – Glazov: GGPI, 2013. – 138 s. (http://maier-rv.glazov.net)
6. Maier R.V. Mnogokomponentnaya model' obucheniya i ee ispol'zovanie dlya issledovaniya didakticheskikh sistem // Fundamental'nye issledovaniya: Pedagogicheskie nauki. – 2013. – N 10. – S. 2524 – 2528.
7. Maier R.V. Osnovnaya zadacha matematicheskoi teorii obucheniya i ee reshenie metodom imitatsionnogo modelirovaniya // Mezhdunarodnyi zhurnal prikladnykh i fundamental'nykh issledovanii. – 2014. – № 2 – S. 36 – 39. URL://www.rae.ru/upfs/?section=content&op=show_article&articleid=5002
8. Solovov A.V., Men'shikov A.A. Diskretnye matematicheskie modeli v issledovaniya protsessov avtomatizirovannogo obucheniya // Educational Technology & Society. – 2001. – N 4. – S. 205 – 210.
|
 Перевести страницу на:
Перевести страницу на:










 Перевести страницу на:
Перевести страницу на:










 Статья опубликована с лицензией Creative Commons Attribution-NonCommercial 4.0 International License (CC BY-NC 4.0) – Лицензия «С указанием авторства – Некоммерческая».
Статья опубликована с лицензией Creative Commons Attribution-NonCommercial 4.0 International License (CC BY-NC 4.0) – Лицензия «С указанием авторства – Некоммерческая».
